I have never been good at time zones, probably because of my poor arithmetic skills caused by New Math in the 1960s. If there’s an 8 involved in a subtraction situation (like GMT -8) then I’m doomed. Bart and I are 8 hours apart in time zones, so that’s swell.
I also have a lot of trouble with Daylight Saving Time. Just the phrase Spring forward, Fall back baffles me. I get tangled up on whether I’m moving forward in time or is the clock moving forward, or maybe both? It got even more complicated when the US decided, in their infinite wisdom, to change to and from Daylight Saving Time at a different time than the rest of the world. That means Bart and I are 8 hours apart, then 7 for a while, back to 8, then 7 again, then back to 8. Drives me bananas.
And don’t even get me started with New Zealand. Since they’re in the southern hemisphere, they go into summer at the opposite time, so we swing wildly apart and closer together by multiple hours. Trying to figure out if Maryanne or Allister are awake or if it’s possibly the following Tuesday is impossible. I’ve been complaining on the NosillaCast about timezones since August of 2009 episode #219!
GMT and UTC
It’s all the rage to talk about time using GMT or UTC. But I find even that confusing.
Did you know that Greenwich, after which Greenwich Mean Time (GMT) is named, does not stay at GMT 0 during Daylight Saving Time? My buddy Ron had been to Greenwich and when I told him that, he did not believe me. Lost his mind when he found out I was right. It’s not that GMT itself changes, it’s that Britain changes to some goofy thing called British Summer Time.
And then there’s Coordinated Universal Time, which is oddly abbreviated UTC. They really do hate us, don’t they? Why do we have GMT and UTC? What is the difference between the two? According to worldtimeserver.com/…, “In short, GMT is an actual time zone, whereas UTC is a time standard that is used to keep time synchronized across the world.”
So UTC is an absolute reference point to keep all clocks in sync, but then why do people give their timezone in UTC if it’s not for timezones? Maybe because you can refer to your timezone as an offset from UTC. Perhaps this explanation from wikipedia will clarify things: “The time zone using UTC is sometimes denoted UTC±00:00 or by the letter Z—a reference to the equivalent nautical time zone (GMT), which has been denoted by a Z since about 1950.” Yeah, totally understand it now.
I will, from this day forward, refuse to use UTC as a timezone just to avoid some time nerd saying to me, “Well actually, UTC means Coordinated Universal Time…” Moving on.
The Problem to be Solved
Why am I bringing all of this up right now? Because our latest assignment in Programming By Stealth is to create a web app for a clock that shows the local time as well as in a time zone of the user’s choosing. I talked about my early success for this assignment in my recent post Programming is My Happy Place.
Believe it or not, creating the local time was pretty darn easy. It turns out that people write libraries that you just point to in your code and they give you super powers. The one we’re using is called moment.js from momentjs.com/…. Once you’ve got it slapped into your code you can do all kinds of fun stuff with times.
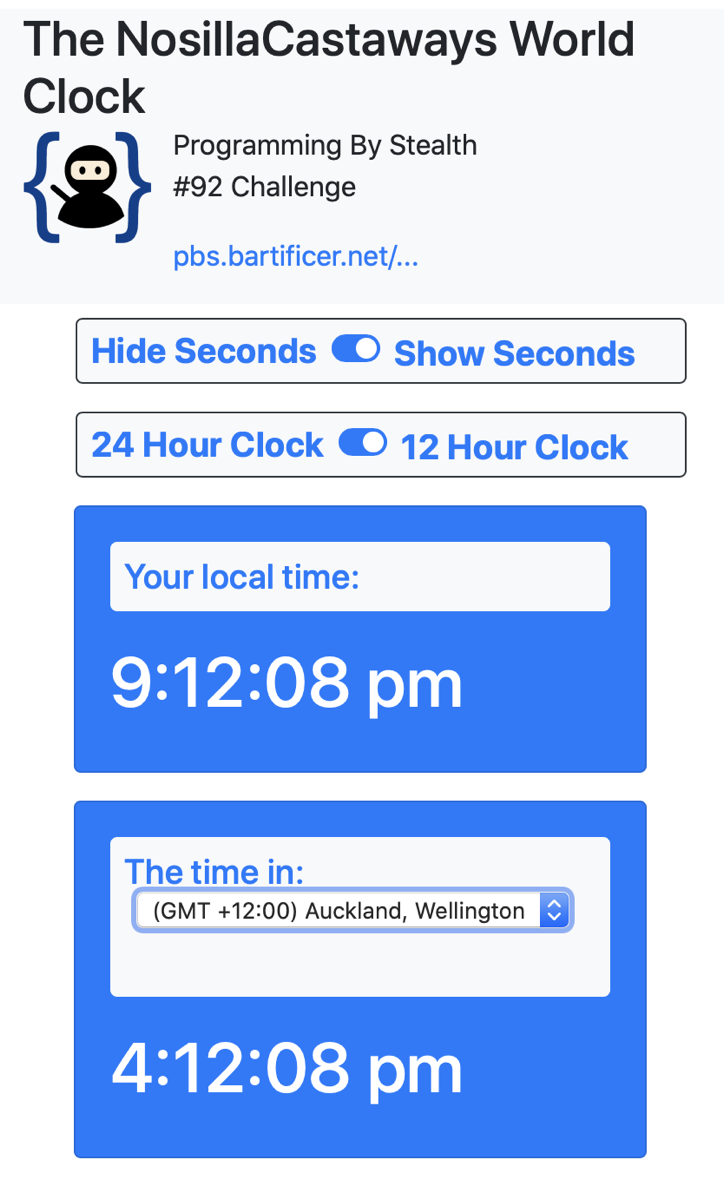
It’s also a really fun assignment because we get to be creative in designing our own interface. Pretty quickly, and without bothering Dorothy at all, I was able to get the user’s local time and it was nice and pretty. Phase two was to add some check boxes so the user could choose whether to show seconds or not and whether to show a 24 or 12-hour clock. A little more challenging but I got that done on my own too.
But then it came time to design the interface to allow the viewer to change time zones. I decided to create a nice little dropdown menu to scroll through to pick the time zone. And this is when things started to get interesting. And by that I mean in the Chinese Proverb “may you have interesting times” kind of way.
How to Display a Selection
Using this swell library I mentioned before, moment.js, there’s a companion library called timezones.js. This library is really cool. You can easily change the time to a different timezone, find times in the past and future, and maybe the time on other planets. I got kind of lost in how many things it can do. But I only need a simple dropdown list of cities and then when you pick a city it would do the magic timezone math in the background and I wouldn’t have to do anything but spit it back out onscreen. Sounds easy enough.
The fine folks who wrote timezones.js have instructions on how to get a list of cities/countries that are supported. I only have to type moment.tz.names(); and it spits out the list. Easy peasy. But there’s a problem. This spits out 493 cities! Can you imagine how annoying that dropdown menu would be? I bet you can’t because it’s worse than you can imagine. Way worse.
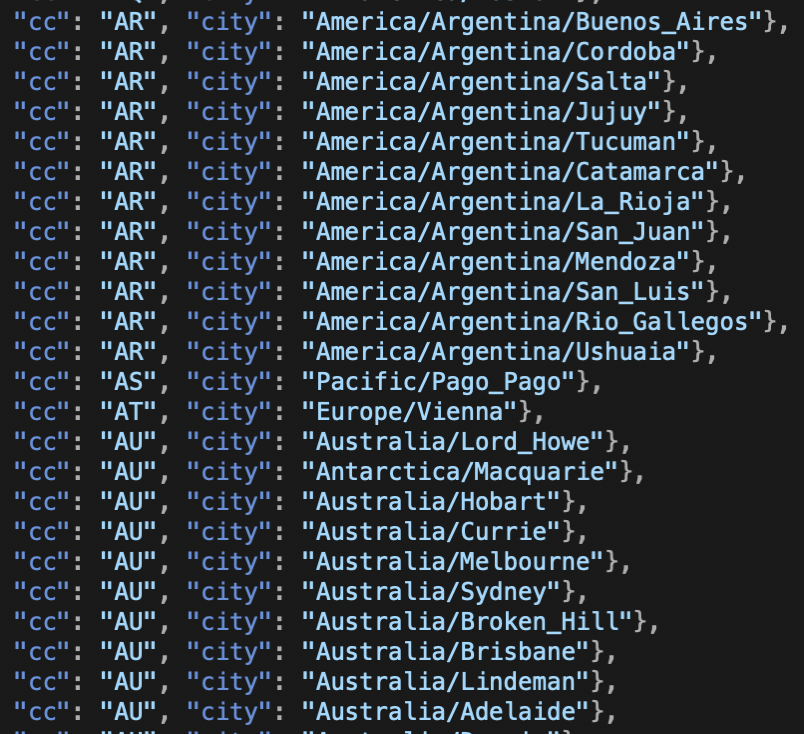
The city names are listed by continent and then city. For example, every city that is in North or South America is prelabled with “America”. So as you’re scrolling through the Americas, Bogota is right next to Boise, Chicago is next to Chihuahua. I know that makes sense alphabetically but if you’re looking for Bogota is that where you would expect to find it?
The good news is that Bart taught us to use Regular Expressions so I could strip out the continent and only have the city names, and I could alphabetize them properly but you’d still have 493 names to go through and that would be nonsense.
I’m not the only one who has ever tried to solve this problem so certainly someone somewhere has a nicer list. All I needed to do was search the Internet for a nice visual listing that made sense to the user, and then I could map it to the timezones my library understood.
I spent four days looking for such a list.
At one point I got desperate and brought up one of those maps that shows the timezones in bands and then little red dots for cities you could tap on within a timezone. I probably spent an hour trying to find one recognizable city name in each timezone while also not only picking just the big countries. I didn’t want all US cities for the half dozen timezones we have for example. It took me a while to realize that this was not going to end in a good list as in many cases I couldn’t even find a city in certain timezones.
Finally I found a list that was way better than the 493 oddly sorted continent/city names. I found a list of “only” 424 city names, but at least they were sorted by country. All of the US was next to each other under the two-character code US, all of Africa was under ZW, you know, nicely sorted like that. It wasn’t ideal but at least it made sense.
I gleefully coded it up and when it was morning in Japan, I excitedly sent it to Kaylee. While she didn’t technically tell me it looked like 🐴💩, she was not at all impressed. Later in the day when Helma in the Netherlands woke up, I got the same reaction. I was crestfallen. I was so proud of my work. But of course they were right, it was ugly and still unintuitive.
Helma is a crazy good programmer and she helpfully suggested I just let people type in the name of a city, then I look it up in the background by latitude and longitude, figure out if it’s summer or winter there and then calculate the time. Yeah, I was not going to do that. The error checking alone on people’s spellings or duplicates would have killed me.
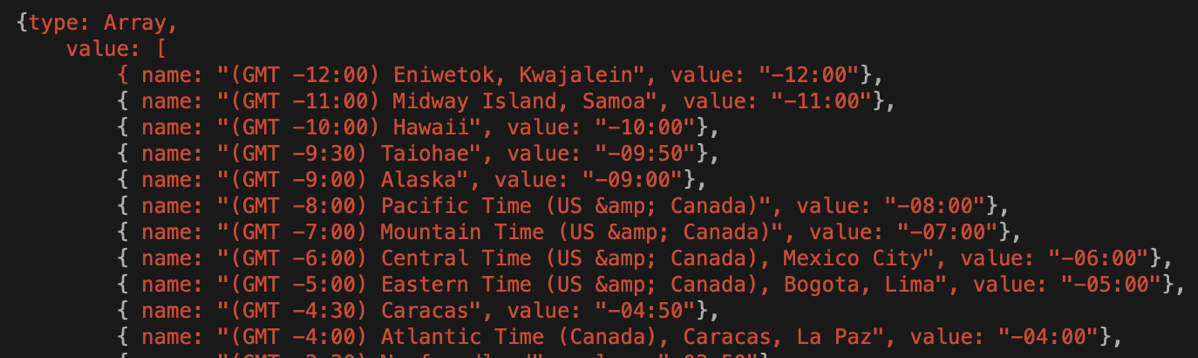
Kaylee did some searching online for a better list and she actually found one that worked. It was released as open source on GitHub by someone who goes by NodeSocket. Here’s what was good about the NodeSocket list. It had the name of the timezone, such as GMT -3:00 followed by a handful of city names from that zone. And it was even sorted by timezone name.
But it was still harder than I thought. The pretty list would only be for the visuals of the dropdown. I would need to map the chosen time zone in the dropdown to a real city name in the official timezone library.
I had to select a city name in a zone from the pretty list, and then do a search in the official timezone library and see if I had a match. For example, for GMT -12:00 it said “Eniwetok, Kwajalein”. Anybody know where the heck those cities are? Me neither. To get the timezone library to understand the time the user wanted, I needed something like a continent or region, followed by a slash and the city name. So I had to copy Eniwetok from this new fancy list and see if it was anywhere in that 493 line long list. Nope, look again.
Copy Kwajalein from the pretty list, check the official list and it’s there! Great. One timezone mapping done. Rinse and repeat 23 more times to get every timezone.
While tedious work, I only needed to find any city match from one list to the other and then my timezone library would work out the rest.
Sometimes though, none of the city names in the pretty list had a match in the timezone library. I had to use more rigorous methods. I actually had to paste the name of a city from the pretty list into a Maps to figure out where it was and see if I could find a city nearby that would be in the same timezone. That made each timezone it’s own little adventure game!

As I worked my way through the timezones in the pretty list, I noticed that the city of Caracas was listed under two different offsets! It was in GMT -4:00, and GMT -4:30. I know I whine a lot about time zones and such but I don’t care who you are, that’s bananas, right? Or a mistake.
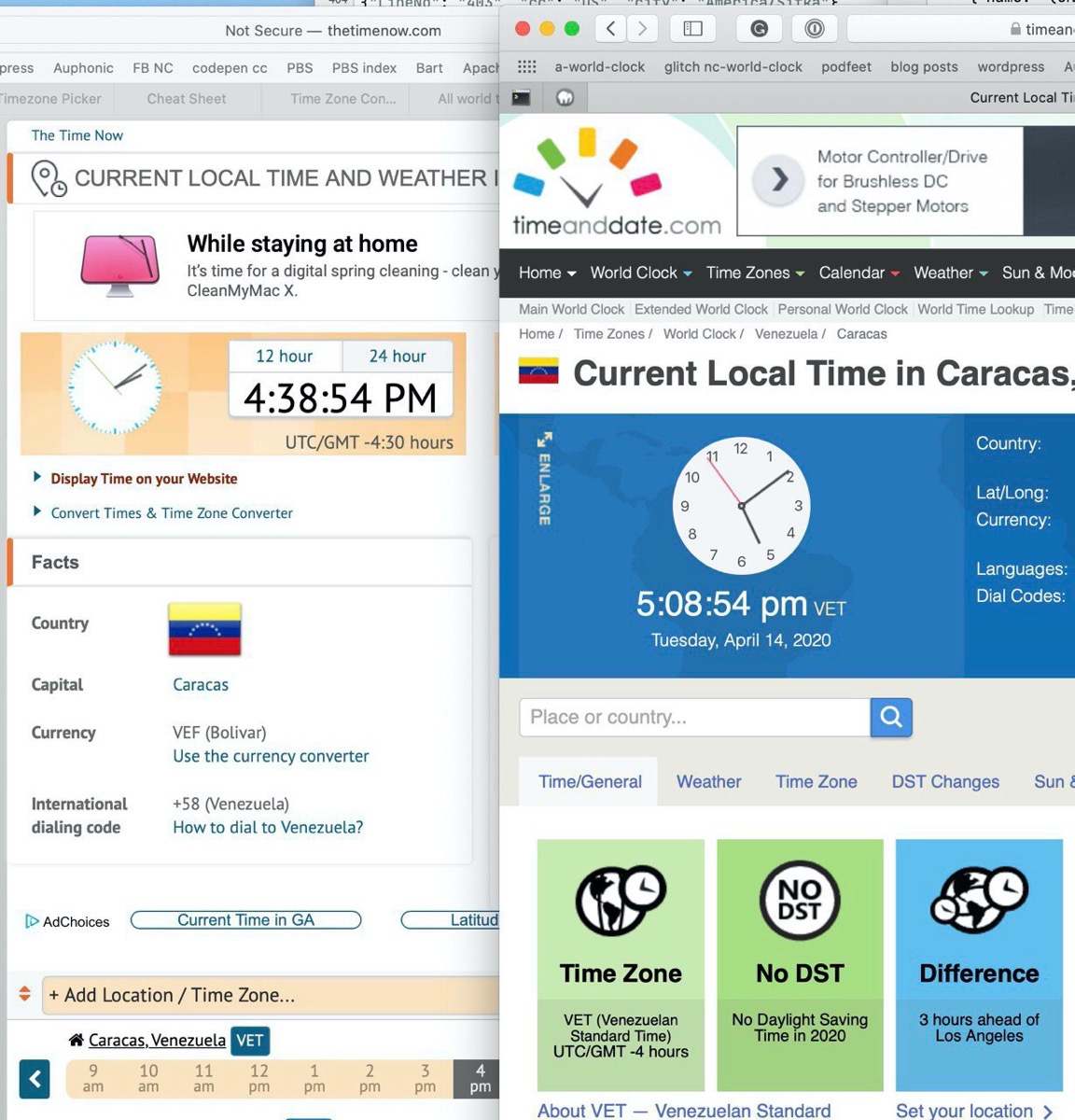
If you ask the Internet what time it is in a city, you’ll find that about 238,427 different web sites are available to try and untangle the mystery of time. I searched for the answer of “what time is it in Caracas?” I got two hits that I thought were particularly interesting. timeanddate.com said it was 5:08pm, while thetimenow.com said it was 4:38pm. Well that’s pretty curious.
I mentioned this curiosity to Kaylee and she found an article from 2016 on www.timeanddate.com/… that may explain the confusion. The article said,
In late 2007 President Hugo Chavez moved Venezuela’s time zone 30 minutes backwards to UTC-4.30, putting all of the country in a half-hour time zone. The change was perceived as a political statement by Chavez, and when Venezuela changes its time in May, there will be no other locations in this UTC offset.
I’m not 100% sure how the person making the pretty list knew that Venezuela had moved back to on the hour but also forgot to remove Caracas from the half hour offset. I decided to go with on the hour for Caracas for my web app, and I hope you’re ok with that.

By the way, 1/2 hour time zone offsets aren’t that unusual. Taiohae out in the South Pacific is on the half hour along with 8 other regions, and the entire country of India. Found that one out when we visited there a few years ago.
But my favorites are the ones that are off by 45 minutes. I mean really, do you have to hate people to do that? Kathmandu in Nepal (where we also visited), Eucla in Australia, and the wee, little Chatham Islands out in the Pacific off of New Zealand also enjoy that 45 minute offset. I cannot imagine if I had to do time math living there!
There’s one more abnormality to this whole thing. I cannot show you what time it is in one specific timezone. That timezone is called Mid-Atlantic and it’s GMT -2:00. My NodeSocket list says simply Mid-Atlantic with no cities. I didn’t immediately give up on GMT -2 though, I did some sleuthing.
If we go back to our friend www.timeanddate.com/… which has a swell map showing timezones and red dots for cities, you can see a couple of red dots out in GMT -2. If you hover over the dots you can find the names of the cities, like Ponta Delgada way out in the Atlantic 900 miles off the coast of Portugal. Fun fact to know and tell, it’s the capital city of the Azores. But guess what? They’ve decided they don’t want to be in that lonely GMT -2:00, they went with plain old GMT with no offset. Maybe because Portugal owns them?
Back to GMT -2:00, we’ve also got Praia, capital city of the island country Cabo Verde sitting right there ready to claim ownership of this lonely timezone. But for no reason I could find, they are in GMT -1:00 instead of -2:00.

And then finally I found one tiny little spot called King Edward Point on South Georgia Island in the South Sandwich Islands which is actually in GMT -2. But here’s the problem, if it’s not acknowledged in the timezones library, then I can’t access it. I may just write a little error check that says, “if someone picks GMT -2, then hard wire in King Edward Point as being 1 hour ahead or behind the next closest timezone”. I’d have to put asterisks all over it because who on earth knows if they honor Daylight Saving Time?
Here’s another questionable fact. The only town I could find on South Georgia Island is called Grytviken which is an abandoned whaling village. It no longer has any permanent residents, but according to Google Maps, it has a Starbucks and a McDonalds. Why do I suspect someone is having fun with Google on this one?
But That was Dumb
After I wrote up this glorious solution, I published the blog post and spammed Twitter, our Facebook group and our Slack Community (podfeet.com/slack). I was exhausted but happy with the relatively simple dropdown that gave valuable information to the user. I’m so glad I publish these blog posts before I talk on the podcast about my discoveries. NuclearJon in our Slack community told me that for some reason Central and Eastern time were reporting the same time.
I checked his screenshots and was able to replicate this error myself. I’m sure many of you have been hollering into your devices at the complete and utterly obvious flaw in the path I took to simplify the list. I took one city in each timezone and made it the definitive source of the time. But it turns out Lima (the city I chose for Eastern) doesn’t observe Daylight Saving Time at the same time as other GMT -5 cities. My entire logic was completely flawed. The time I was showing in Lima was correct for Lima but was not correct for US cities in the same GMT offset.
The only way to do this right is to show you all of the cities in every timezone, or to choose for you which cities you’re allowed to query and allow no general assumptions to be made.
Back to the Drawing Board
I went back to the library, had it spit out all of the cities, and actually used Excel to format the data. I know, I should have used regular expressions, but I know how to do multiple modifications at once in Excel. I pulled in the data to a single column, used Text to Columns to get just the bit I wanted, then added columns with the common info for each element, like , "name", and then I concatenated the city names and the GMT offset column with the other formatting stuff. Of course I then had to do a copy, paste special and only keep the values (so it was strings, not formulas). From there I exported it as a Comma Separated Value (CSV) file and was able to make it into a nice JSON file by adding the square brackets around all the data to make it an array. Easy peasy, right?
Then I noticed that the official data list had a bunch of entries that said Etc/GMT, Etc/GMT+0, Etc/GMT0, Etc/GMT+0, and on and on like that. I deleted them all. When I was finished, the list now has 539 cities, sorted by GMT offset.
I do hope you appreciate the exhaustive lengths I have gone to in order to ensure the veracity of the data behind my clock web app AND to bring you a list that makes sense and is easy to scroll through to find the time zone you seek.
But It’s a Lie
Sadly, the list is a lie. If you choose GMT -8 from my list, you will find the time in Los Angeles. But right now, we’re not at GMT -8, we’re at GMT -7 because of Daylight Saving Time. Some places aren’t in Daylight Saving Time right now so their GMT offsets might be right! I know there’s not an easier way to show this but it still feels like I’m misleading the user. Everyone I’ve shown it to says I shouldn’t worry about it because everyone does it, but it still bothers me.
Bottom Line
I’m having a ball writing this web app and if you’d like to watch it as I’m working on it, you can view it at https://nc-world-clock.glitch.me.
If you want so watch something really entertaining, please watch the YouTube video NuclearJon posted entitled “The Problem with Time & Timezones” by Computerphile. It is an absolutely hysterical and completely accurate explanation of the madness that is working with time and timezones.

